Der Tangens des (orientierten) Winkels \(\alpha\) zwischen der positiven x-Richtung und einer Geraden ist die Steigung \(m\) dieser Geraden.
\[\fcolorbox{green}{white}{$tan\,\alpha=\frac{\Delta y}{\Delta x}=m$}\]
Mithilfe des nachfolgenden GeoGebraApplets kann der Einfluss der Höhe \(h\) auf die Steigung \(m\) sowie auf das Maß des Neigungswinkels \(\alpha\) der Geraden untersucht werden.
Arbeitsblatt "Einführung Tangens" Lösung zu "Einführung Tangens" Lösung zu WESTERMANN Mathematik 10II 52/5 Lösung zu WESTERMANN Mathematik 10II 52/6
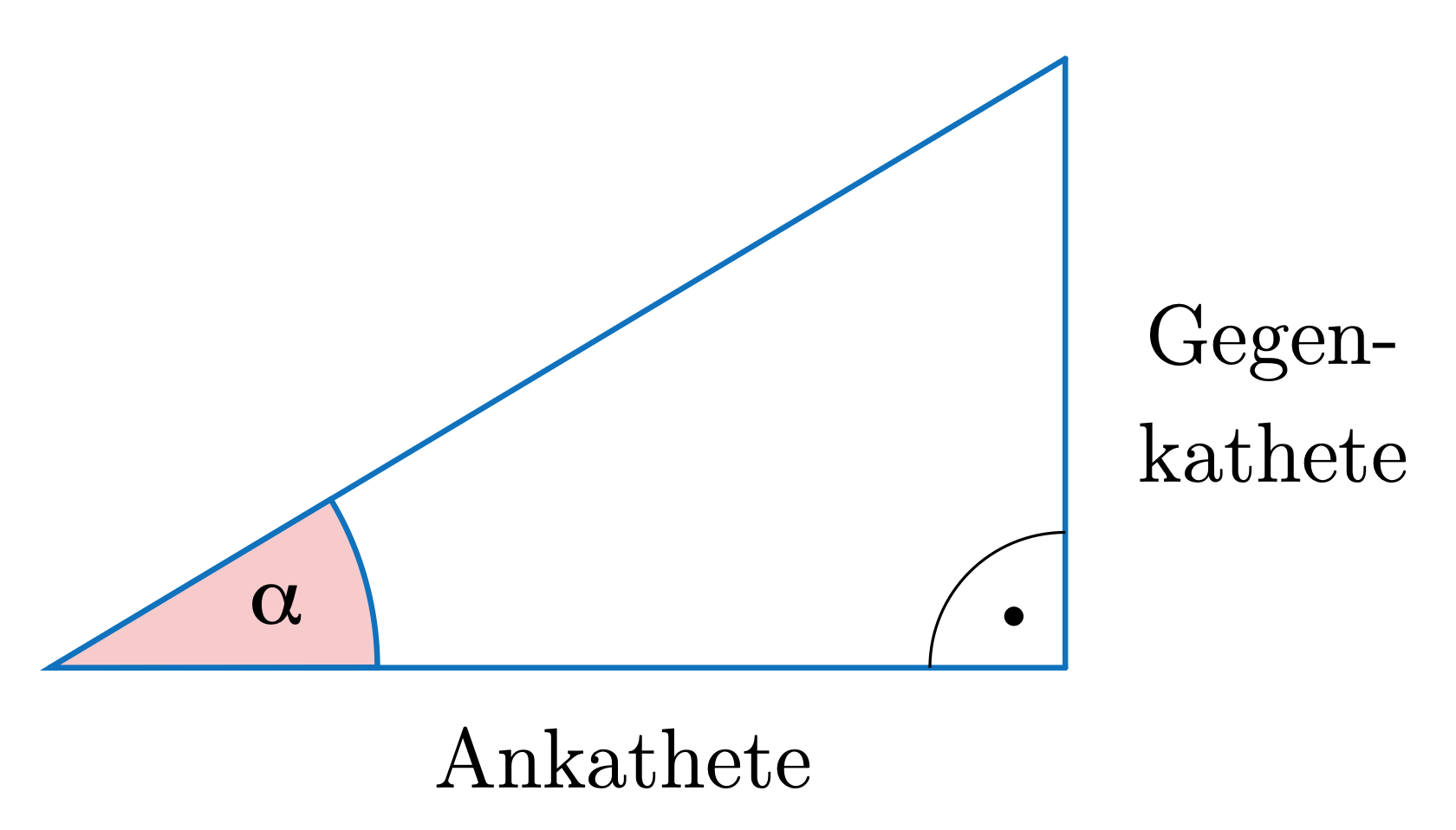
In einem rechtlinkligen Dreieck gilt für den Tangens eines Winkels \(\alpha\):
\[\fcolorbox{green}{white}{$tan\,\alpha=\frac{L\ddot{a}nge\,der\,Gegenkathete}{L\ddot{a}nge\,der\,Ankathete}$}\]
Mithilfe dieses Zusammenhangs können nun im rechtwinkligen Dreieck Berechnungen durchgeführt werden.
Dabei geht man wie folgt vor:
Info "Tangens am rechtwinkligen Dreieck" Lösung zu WESTERMANN Mathematik 10II 53/1 Lösung zu WESTERMANN Mathematik 10II 53/2 Lösung zu WESTERMANN Mathematik 10II 53/3 Lösung zu WESTERMANN Mathematik 10II 53/4
Mithilfe der Steigung einer Geraden und dem Tangens kann der Winkel zwischen der Geraden und der x-Achse berechnet werden.
► Lösung zu WESTERMANN Mathematik 10II 55/4
Ebenso kann mithilfe der Steigung und dem Tangens der Winkel zwischen zwei Geraden berechnet werden.
► Arbeitsblatt: "Winkel zwischen zwei Geraden"
► Lösung zu "Winkel zwischen zwei Geraden"
► Lösung zu WESTERMANN Mathematik 10II 56/2
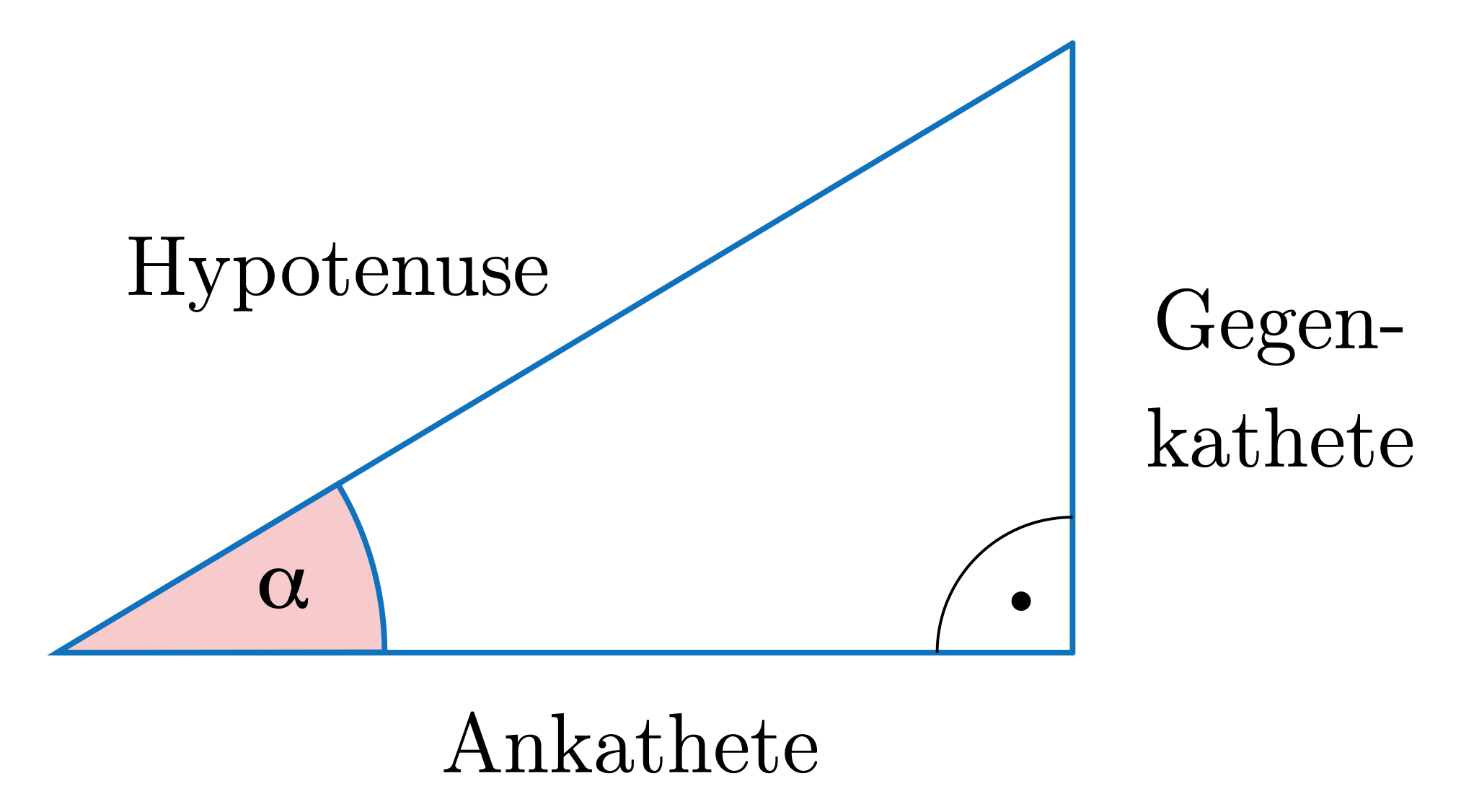
Neben dem Tangens eines Winkels \(\alpha\) sind in einem rechtlinkligen Dreieck weitere Verhältnisse (Quotienten) definiert: \[\fcolorbox{green}{white}{$sin\,\alpha=\frac{L\ddot{a}nge\,der\,Gegenkathete}{L\ddot{a}nge\,der\,Hypotenuse}$}\] \[\fcolorbox{green}{white}{$cos\,\alpha=\frac{L\ddot{a}nge\,der\,Ankathete}{L\ddot{a}nge\,der\,Hypotenuse}$}\]
Info: "Einführung Sinus und Kosinus" Lösung zu WESTERMANN Mathematik 10II 58/4 Lösung zu WESTERMANN Mathematik 10II 58/5 Lösung zu WESTERMANN Mathematik 10II 58/6