Eine Gleichung der Form \(ax^2+bx+c=0\) mit \(a≠0\) bezeichnet man als quadratische Gleichung. In einer quadratischen Gleichung ist die Variable (Unbekannte) \(x\) in der zweiten Potenz (im Quadrat) enthalten. Die Zahlen \(a\), \(b\) und \(c\) bezeichnet man als Koeffizienten.
Gilt zusätzlich \(b=0\), bezeichnet man die Gleichung als eine reinquadratische Gleichung: \(ax^2+c=0\).
Grundsätzlich unterscheidet man drei Fälle:
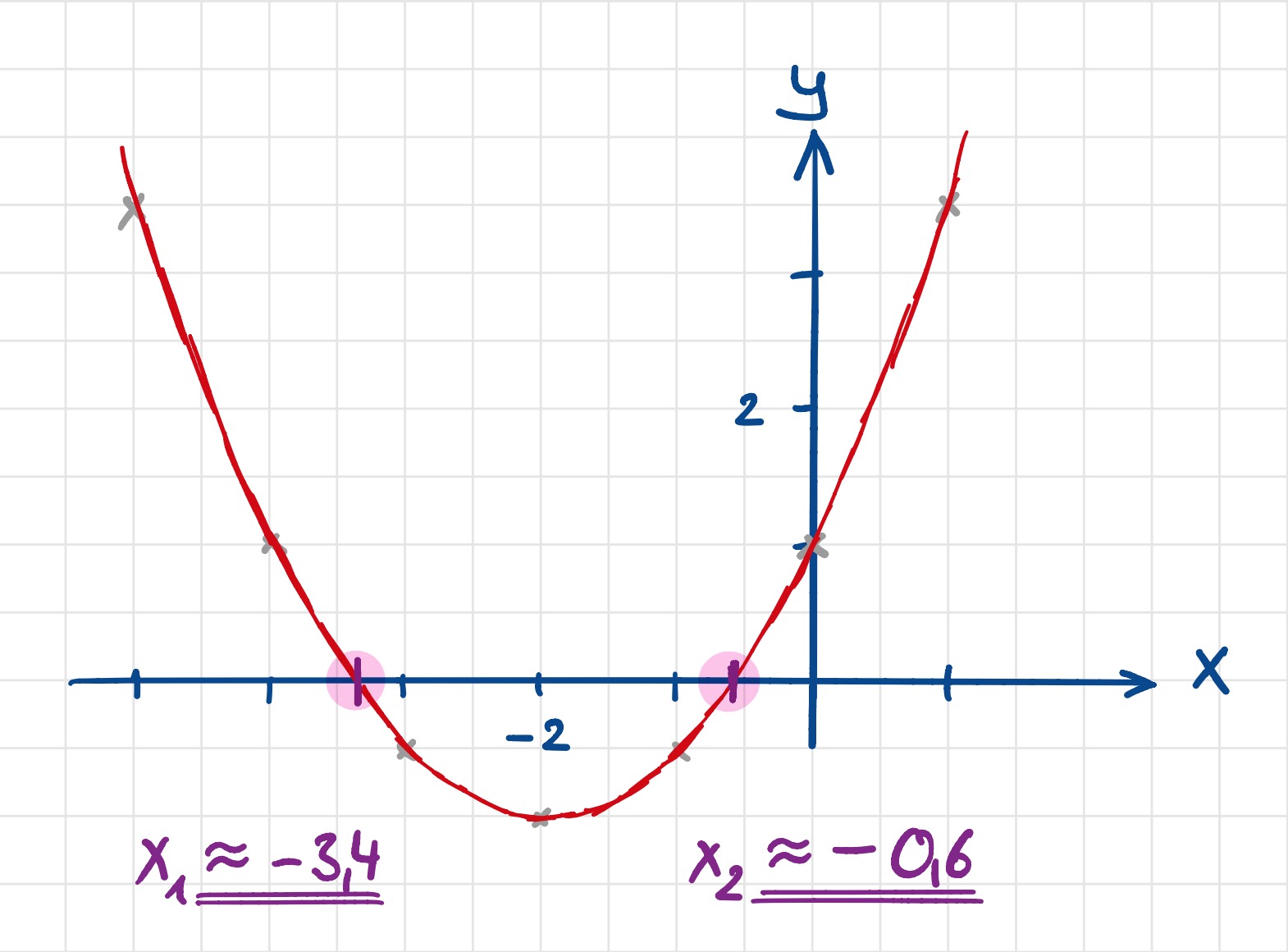
Am einfachsten lässt sich eine quadratische Gleichung graphisch (zeichnerisch) lösen. Die Lösungen der quadratischen Gleichung entsprechen dabei den Nullstellen der zugehörigen Parabel \(y=ax^2+bx+c\).
Rechnerisch lösen lässt sich eine quadratische Gleichung durch Äquivalenzumformungen. An besten funktioniert dies bei reinquadratischen Gleichungen oder wenn die Gleichung in Scheitel(punkt)form vorliegt.
► Arbeitsblatt: "Lösung durch Äquivalenzumformung"
► Lösung zu: "Lösung durch Äquivalenzumformung"
Eine andere Möglichlichkeit zum Lösen von quadratischen Gleichungen stellt die Anwendung der sog. Lösungsformel für quadratische Gleichungen ("Mitternachtsformel") dar. Diese wird bevorzugt dann angewandt, wenn die quadratische Gleichung in der Form \(ax^2+bx+c=0\) vorliegt.
Dazu liest man die Koeffizienten \(a\), \(b\) und \(c\) ab und setzt sie in die Formel \[x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\] ein.
Der Term \(D=b^2-4ac\) wird als Diskriminante bezeichnet. Die Diskriminante entscheidet darüber, wieviele Lösungen die quadratische Gleichung hat:
► Arbeitsblatt: "Die Lösungsformel"
► Lösung zu: "Die Lösungsformel"
► Info: "Schnittpunkte von Funktionsgraphen"
► Lösung zu WESTERMANN Mathematik 10II 44/4
► Lösung zu WESTERMANN Mathematik 10II 44/8