►
►
►
►
►
►
►
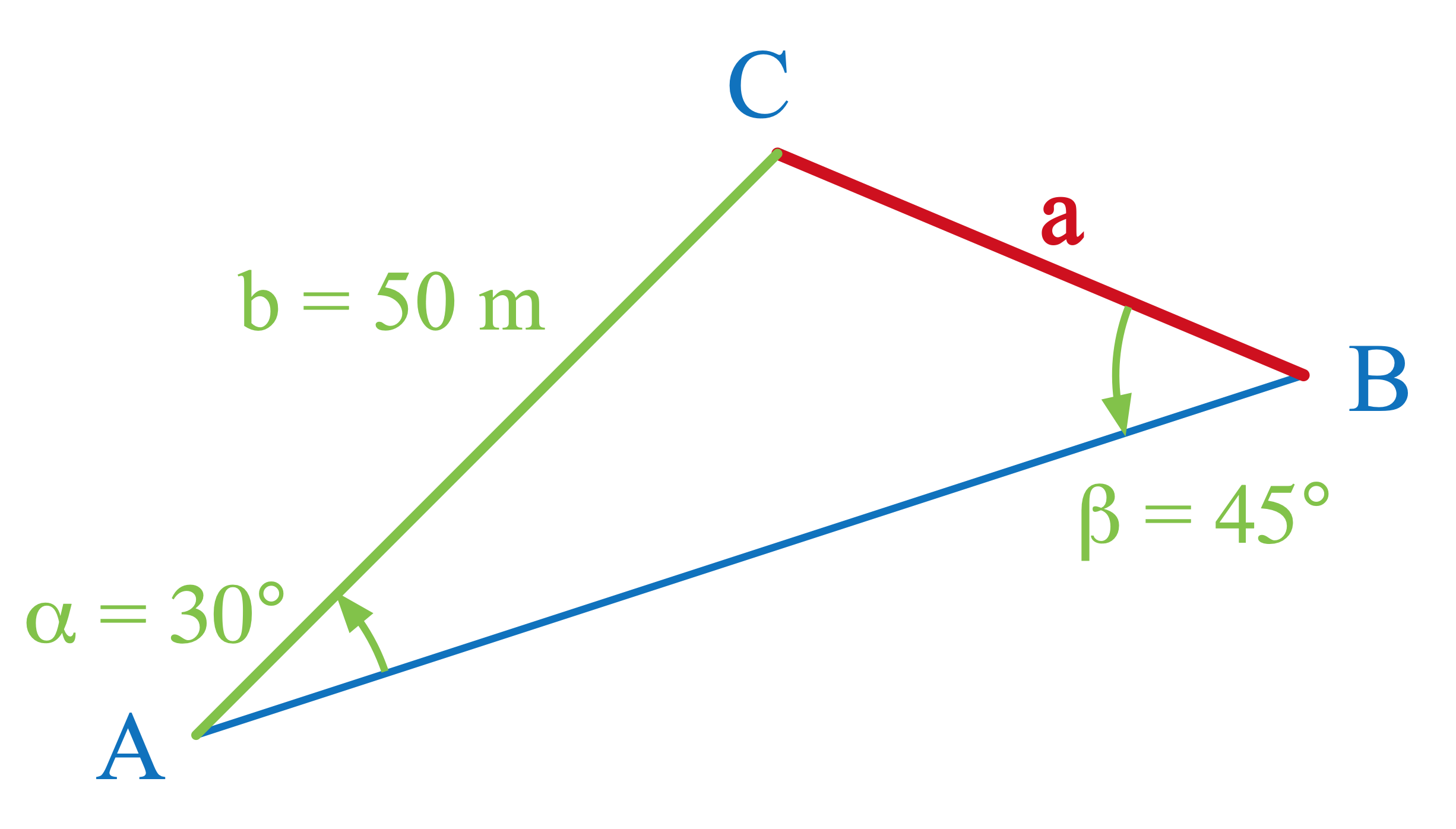
In einem Dreieck sind die Verhältnisse aus der Länge einer Seite zum Sinus des gegenüberliegenden Winkels stets gleich:
\[\fcolorbox{green}{white}{$\frac{a}{\sin\,\alpha}=\frac{b}{\sin\,\beta}$}\]
► Info: "Herleitung Sinussatz"
► Beispiele zu "Berechnungen mit dem Sinussatz"
► Lösung zu "Berechnungen mit dem Sinussatz"
► Lösung zu WESTERMANN Mathematik 10II 74/3
► Lösung zu WESTERMANN Mathematik 10II 75/6 a-c
► Lösung zu WESTERMANN Mathematik 10II 75/6 d-f
► GeoGebraApplet zur Aufgabe 75/6 d
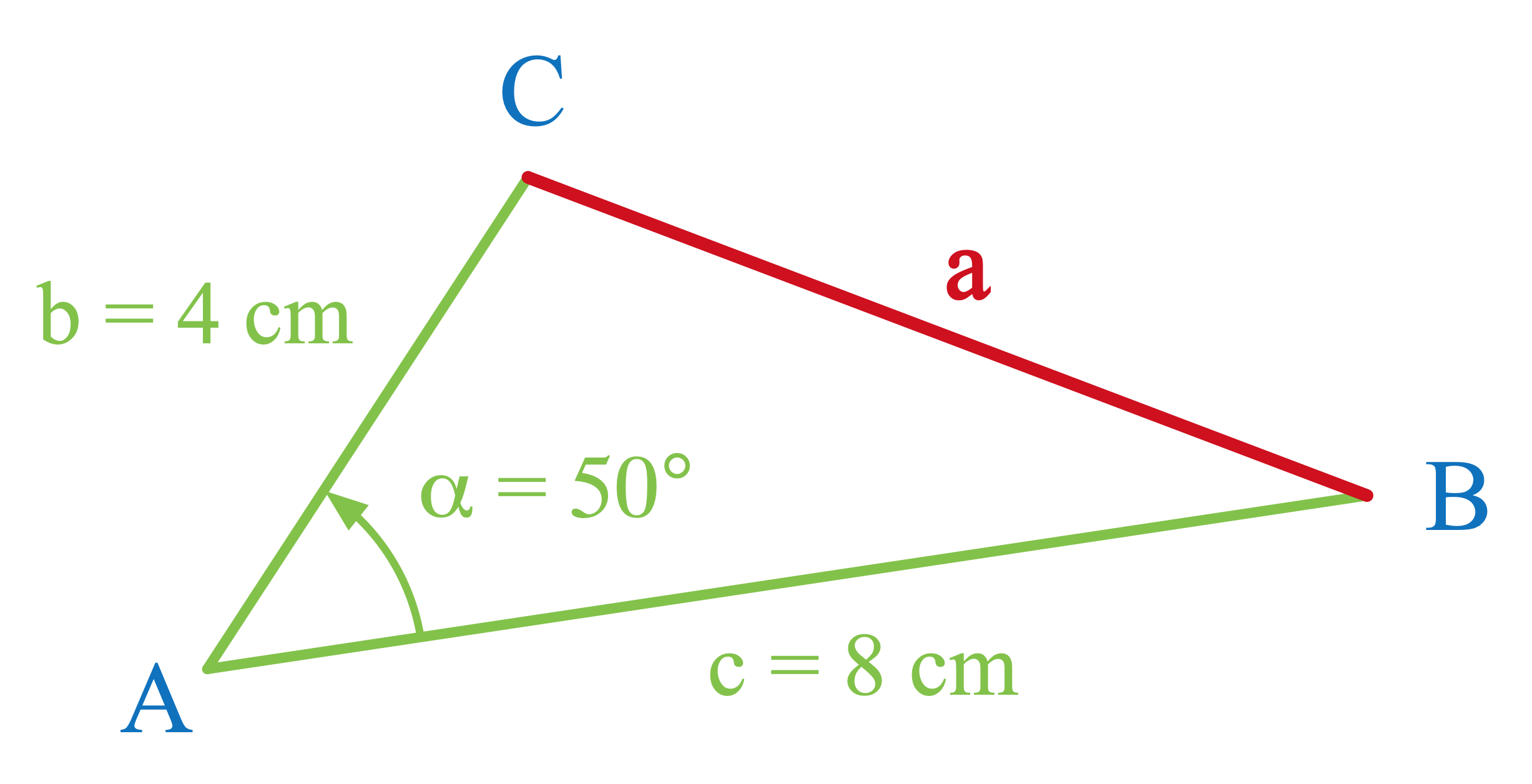
In einem beliebigen Dreieck ABC gilt für zwei Seitenlängen und das Maß des dazwischenliegenden Winkels:
\[\fcolorbox{green}{white}{$a^2=b^2+c^2-2\cdot b\cdot c\cdot \cos\,\alpha$}\]
► Beispiele zu "Berechnungen mit dem Kosinussatz"
► Lösung zu "Berechnungen mit dem Kosinussatz"
► Lösung zu WESTERMANN Mathematik 10II 77/3
► Lösung zu WESTERMANN Mathematik 10II 78/2
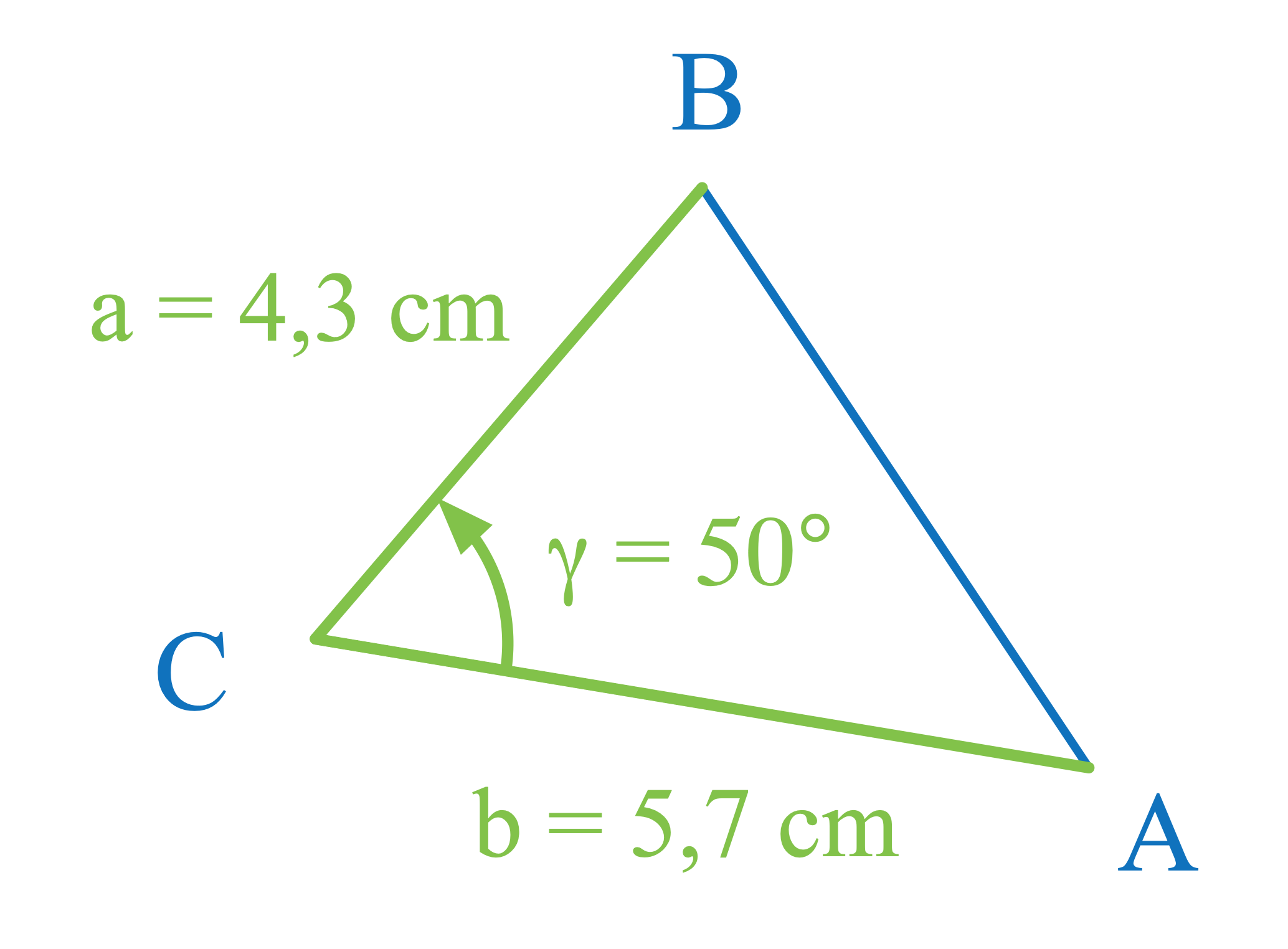
Der Flächeninhalt eines Dreiecks kann aus den Längen zweier Seiten und dem Maß des dazwischenliegenden Winkels berechnet werden:
\[\fcolorbox{green}{white}{$A=\frac{1}{2}\cdot a\cdot b\cdot \sin\,\gamma$}\]
► Herleitung "Flächeninhalt eines Dreiecks"
► Lösung zur Herleitung "Flächeninhalt eines Dreiecks"
► Lösung zu WESTERMANN Mathematik 10II 79/3
Nebenstehende Übersicht zeigt ein Struktogramm für die Anwendung von Sinus, Kosinus und Tangens sowie des Sinus- und Kosinussatzes im Dreieck bei verschiedenen Konstellationen der (vor-)gegebenen Größen.
► Übersicht "Berechnungen in Dreiecken“
► Wiederholung "Kongruenzsätze“
Nachfolgend sind exemplarisch einige Aufgaben zum Thema Ebene Geometrie aus dem Teil A der Abschlussprüfung dargestellt.
► Abschlussprüfung "Ebene Geometrie“ (2015 HT - A1, 2019 HT - A1, 2012 HT - A1, 2011 HT - A3)
► Lösung zur Abschlussprüfung "AP MII 2015 HT - A1“
► Lösung zur Abschlussprüfung "AP MII 2019 HT - A1“
► Lösung zur Abschlussprüfung "AP MII 2012 HT - A1“
► Lösung zur Abschlussprüfung "AP MII 2011 HT - A3“
Für weitere Abschlussprüfungen zum Thema Ebene Geometrie vgl. die nachfolgende Übersicht und die
Homepage des ISB.
Mit nachfolgendem Kompetenztest kann der sichere Umgang mit dem Sinus- und dem Kosinussatz bei der Berechnungen in allgemeinen Dreiecken überprüft werden.
► Kompetenztest "Berechnungen in Dreiecken"